Loi de Benford
La détection des fraudes comptables
Article paru dans la Revue Française de Comptabilité n°321 d'avril 2000, et écrit par :
Xavier LABOUZE
Maître de Conférences de Statistiques à l'Université Paris XI, Docteur ès Sciences, Ingénieur INPG.
[email protected]
Robert LABOUZE
Ingénieur Centralien, Diplômé d'Expertise Comptable
[email protected]
Résumé de l'article
Il existe, depuis plus de 100 ans, un outil simple et puissant, pour détecter les fraudes dans des comptes à auditer, un outil déjà utilisé aux Etats-Unis et qui gagnerait à être mieux connu en France.
L'objet de cet article est donc, après avoir décrit brièvement l'historique de la découverte (dès 1881) de l' étonnante Loi de Benford et de sa démontration mathématique, bien que tardive ( seulement en 1996), de montrer comment il est possible, simplement en utilisant un test d'hypothèse, basé sur la Loi du Khi Deux, de mettre en évidence l'existence d'une fraude avec un risque de se tromper au plus égal à 5 %.
D'après la Loi de Benford, il ressort que le premier chiffre de tout nombre résultant d'une mesure (exprimée en francs ou en euros, dans notre cas ) a environ 6 fois plus de chances d'être un " 1 " qu'un " 9
Avertissement des auteurs
Cet article n'a pas pour but de développer les techniques statistiques de contrôle par sondage ( qui sont supposées connues pour l'essentiel : échantillonnage, extrapolation de l'échantillon à l'ensemble de la population, interprétation statistique des résultats ainsi extrapolés, en terme d'estimation des paramètres de la population ). Nous supposerons également connus les tests d'hypothèses et l'interprétation des observations faites sur un échantillon pour conclure au rejet ou à l'acceptation de l'hypothèse testée.
Le but de cet article sera plutôt de montrer comment une loi étonnante peut fournir à l'auditeur, quel qu'il soit, un nouvel outil performant pour le guider dans la mise en évidence de zones sensibles où des fraudes ont très probablement été commises.

| Loi de Benford | ||||||
|---|---|---|---|---|---|---|
|
||||||
| Article paru dans la Revue Française de Comptabilité n°321 d'avril 2000, et écrit par : | ||||||
|
|
||||||
| Résumé de l'article | ||||||
Il existe, depuis plus de 100 ans, un outil simple et puissant, pour détecter les fraudes dans des comptes à auditer, un outil déjà utilisé aux Etats-Unis et qui gagnerait à être mieux connu en France. L'objet de cet article est donc, après avoir décrit brièvement l'historique de la découverte (dès 1881) de l' étonnante Loi de Benford et de sa démontration mathématique, bien que tardive ( seulement en 1996), de montrer comment il est possible, simplement en utilisant un test d'hypothèse, basé sur la Loi du Khi Deux, de mettre en évidence l'existence d'une fraude avec un risque de se tromper au plus égal à 5 %. D'après la Loi de Benford, il ressort que le premier chiffre de tout nombre résultant d'une mesure (exprimée en francs ou en euros, dans notre cas ) a environ 6 fois plus de chances d'être un " 1 " qu'un " 9 |
||||||
Avertissement des auteurs |
||||||
Cet article n'a pas pour but de développer les techniques statistiques de contrôle par sondage ( qui sont supposées connues pour l'essentiel : échantillonnage, extrapolation de l'échantillon à l'ensemble de la population, interprétation statistique des résultats ainsi extrapolés, en terme d'estimation des paramètres de la population ). Nous supposerons également connus les tests d'hypothèses et l'interprétation des observations faites sur un échantillon pour conclure au rejet ou à l'acceptation de l'hypothèse testée. Le but de cet article sera plutôt de montrer comment une loi étonnante peut fournir à l'auditeur, quel qu'il soit, un nouvel outil performant pour le guider dans la mise en évidence de zones sensibles où des fraudes ont très probablement été commises. |
||||||
![]()
Un peu d'histoire
![]()
A l'époque où les calculatrices n'existaient pas, les calculs se faisaient, à la main, à l'aide de tables. Un jour de 1881, un astronome américain, Simon NEWCOMB, s'aperçut que les premières pages d'une table de logarithmes étaient plus usées que les autres. Se pouvait-il que les données recherchées dans cette table commençaient plus souvent par le chiffre "1" ? Il tenta de résumer les résultats de son observation dans une formule simple pour mesurer la fréquence d'apparition du premier chiffre C, celui situé le plus à gauche, dans un ensemble de données :
|
|
A l'époque, cette formule ne convainquit personne.
Cinquante ans plus tard, vers 1938, un physicien américain, Frank Benford, redécouvrit les mêmes fréquences que celles résultant de l'application de la formule de Newcomb, en répertoriant plus de 20 000 données sélectionnées dans des domaines aussi divers que les longueurs de plus de 300 fleuves, les recensements démographiques de plus de 3 000 régions, les masses atomiques des éléments chimiques, les cours de bourse, les constantes de la physique, les couvertures de journaux, etc.
Il constata, donc, que le premier chiffre était un "1" près d'une fois sur trois ! Il en fit une loi qui porte aujourd'hui son nom : la Loi de BENFORD.
La Loi de Benford, enfin démontrée en ... 1996
![]()
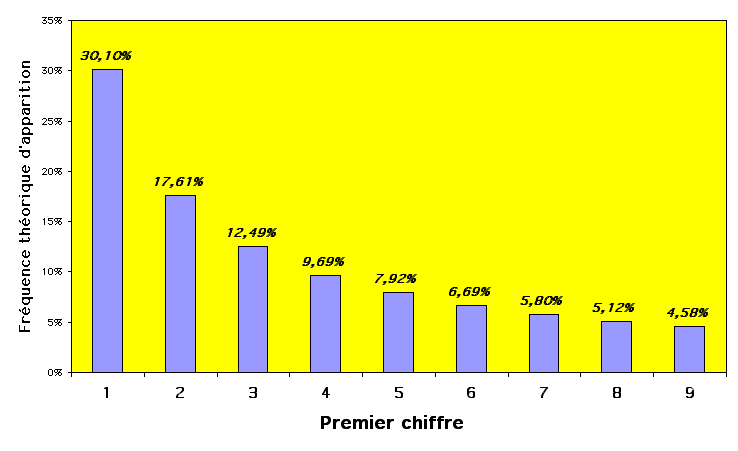
Ce n'est qu'en 1996 que Terence HILL démontra mathématiquement la loi de Benford. Cette démonstration part du principe que tous les nombres incriminés sont exprimés dans une certaine unité. Mais s'il existe une loi universelle des premiers chiffres, elle doit être indépendante de l'unité choisie. Cela suffit à Benford et à ses successeurs pour trouver la fréquence théorique d'apparition du premier chiffre d'un nombre.
![]()
Application aux données comptables
![]()
Les contrôleurs fiscaux américains s'appuient sur cette loi pour détecter des fraudes fiscales : en effet, des données falsifiées suivent rarement une loi de Benford .
En France, les commissaires aux comptes pourraient en faire de même. Pour cela, voici la méthode pratique et statistique que nous vous suggérons d'appliquer.
1ère étape : Phase d'analyse
![]()
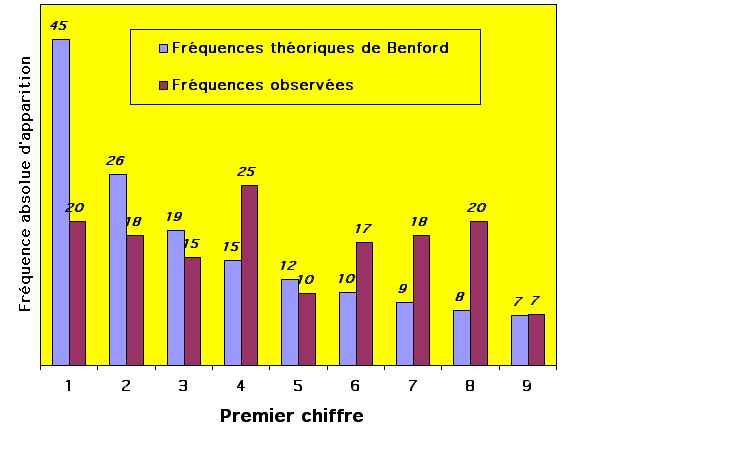
Sur un échantillon prélevé rigoureusement au hasard d'un document à contrôler (journal, compte de grand-livre, balance ou état d'inventaire), on repère tous les premiers chiffres de chaque montant (quel que soit son nombre de chiffres) et l'on établit un tableau de fréquences, conformément au modèle ci-dessous.
Par exemple, considérons un échantillon composé de N =150 montants exprimés en francs ou en euros, parmi lesquels nous observons, par exemple, 20 montants commençant par le chiffre " 1 ", 18 commençant par " 2 ", etc.
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
2è étape : Phase de test
![]()
Nous sommes en présence d'une distribution de fréquences observées. Notre méthode va consister à émettre une hypothèse sur la distribution théorique suivie par la population d'où l'échantillon a été extrait, et à comparer ces deux distributions pour savoir si les écarts constatés entre elles sont significatifs ou simplement dus aux fluctuations d'échantillonnage.
L'hypothèse, selon laquelle il n'y a pas d'écarts significatifs entre les deux distributions ( c'est-à-dire les fréquences observées sur l'échantillon sont proches des probabilités théoriques tirées de la Loi de Benford ) doit être testée et fixer à 5 % au plus le risque de se tromper en rejetant cette hypothèse.
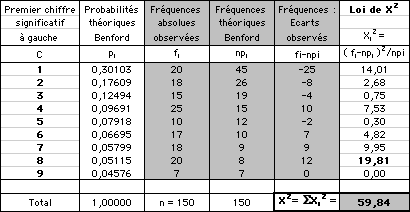
Pour ce faire, nous allons relever, pour chaque premier chiffre, les différences constatées entre les fréquences observées et les fréquences théoriques, et appliquer le test du kHI DEUX (X2) pour mettre en évidence le caractère significatif ou non de ces différences.
L'application du test sur l'exemple proposé fait ressortir les résultats suivants :
|
|
|
![]()
3è étape : Phase de conclusion
![]()
Sous l'hypothèse Ho, ( Ho = il n'y a pas de différence entre les fréquences observées et celles résultant de l'application de la Loi de Benford ), les montants contrôlés doivent suivre la Loi de Benford. Ce qui doit conduire à observer une somme des valeurs de X2 (calculées pour chaque premier chiffre C observé avec la fréquence indiquée), inférieure au seuil de 15,50 (correspondant à la valeur tabulée d'une loi de Khi deux, au risque de 5%, avec huit degrés de liberté - c'est-à-dire les neuf chiffres de 1 à 9, diminués d'une unité -), avec un risque de se tromper au plus égal à 5 % : comme cette somme X2 est égale à 59,84, supérieure à 15,50, l'hypothèse est refusée. On en déduit qu'il y a eu certainement un biais.
On peut admettre que la
quantité " ÷(
X2 ) - ÷(2v
- 1) " suit une loi normale
réduite.
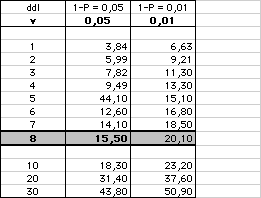
Si les résultats avaient été différents et la somme X2 inférieure à 15,50, on n'aurait pas pu rejeter l'hypothèse Ho et donc rien n'aurait pu s'opposer à son acceptation ( ce qui ne constitue pas, en soi, la preuve qu' aucun biais n'existe ).
4è étape : Recherche des éléments probants
![]()
Si l'hypothèse est rejetée, seul cas intéressant à étudier, il y a donc un biais, et les données observées sur l'échantillon nous amènent à rejeter l'hypothèse selon laquelle les données dans la population suivent une Loi de Benford, et,en affirmant celà, nous avons au plus 5 % de chances de nous tromper.
Tout le travail de l'auditeur va maintenant consister à localiser les données qui contredisent la Loi de Benford . Il conviendra donc de :
- Dans un premier temps, repérer, sur l'échantillon, les valeurs de X2 qui contribuent le plus au dépassement du seuil de 15,50. Dans le cas présent, un certain nombre de montants commençant par 8 sont à l'évidence erronés, puisqu'ils contribuent pour 19,81 au franchissement du seuil de 15,50 ;
- Dans un deuxième temps, mettre en évidence, toujours sur l'échantillon, les montants litigieux dont il faudra rechercher les causes, les éléments probants et en déduire une première estimation sur l'échantillon ;
- Dans un troisième temps, extrapoler à la population tout entière l'estimation de la différence totale avec un certain niveau de confiance ( 95 % ) ;
- Enfin, rechercher, dans la population, les éléments probants démontrant que la fraude est effective et étayée par des pièces comptables et/ou des témoignages sans aucune ambiguïté.
La mise en place de cette nouvelle procédure de contrôle ne modifie en rien les méthodes habituellement utilisées. Elle ajoute seulement un outil supplémentaire simple et performant dont il serait dommage de se priver.
Références bibliographiques
![]()
Publications françaises
1) Revue " La Recherche " n° 316 de Janvier 1999
D'après un article de Ted HILL, publié dans la revue American Scientist n° 86 de 1998
On peut trouver cet article, en français, sur le site Internet de la revue " La Recherche " : http://www.larecherche.fr
Mais également, en anglais, sur le site : http://www.sigmaxi.org/amsci/articles/98articles/hill.html
2) Un autre site suisse, mais avec des textes en anglais, sauf la présentation qui est en français : http://www.jura.ch/lcp/cours/dm/benford/benford.html
3) L'émission Archimède du 29/12/98 sur Arte, que l'on trouve sur le site Internet de Arte à l'adresse :
http://www.arte-tv.com/hebdo/archimed/19981229/ftext/sujet7.html
Publications américaines
1) Sur le site Internet de " WOLFRAM Research ", à l'adresse : http://mathworld.wolfram.com/Digit.html , on trouvera une abondante bibliographie sur le sujet, notamment les articles suivants :
2) NIGRINI N. " A taxpayer Compliance Application of Benford's Law " ( Article paru dans J. Amer. Tax. Assoc. N° 18 de 1996 ) ;
3) MATTHEWS R. " The Power of One ", article paru dans NewScientist de Juillet 1999 : on peut trouver le texte intégral de l'article sur Internet à l'adresse : http://www.newscientist.com/ns/19990710/thepowerof.html
4) HILL T.P. De nombreux articles parus de 1995 à 1998.
Pour actualiser ces références bibliographiques, nous recommandons d'utiliser le moteur de recherche Google (http://www.google.fr) avec les mots-clés suivants : "Benford's Law " ou " Digital analysis ".
![]()